ICPC冬令营Day03

计算几何+概率论初步

A - Birthday Cake

​ Lucy and Lily are twins. Today is their birthday. Mother buys a birthday cake for them. Now we put the cake onto a Descartes coordinate. Its center is at (0, 0), and the cake’s length of radius is 100. There are 2N (N is a integer, 1 ≤ N ≤ 50) cherries on the cake. Mother wants to cut the cake into two halves with a knife (of course a beeline). The twins would like to be treated fairly, that means, the shape of the two halves must be the same (that means the beeline must go through the center of the cake) , and each half must have N cherrie(s). Can you help her?

Note: the coordinate of a cherry (x, y) are two integers. You must give the line as form two integers A, B (stands for Ax + By = 0) each number mustn’t in [−500, 500]. Cherries are not allowed lying on the beeline. For each dataset there is at least one solution.

Input

The input file contains several scenarios. Each of them consists of 2 parts: The first part consists of a line with a number N, the second part consists of 2N lines, each line has two number, meaning (x, y). There is only one space between two border numbers. The input file is ended with N = 0.

Output

For each scenario, print a line containing two numbers A and B. There should be a space between them. If there are many solutions, you can only print one of them.

Sample Input

2
-20 20
-30 20
-10 -50
10 -5
0

Sample Output

0 1

题目分析：

简单几何题，给出一个以(0,0)为圆心，半径为100的圆，给出一个数字N，然后给出2*N个坐标系上点的坐标，求出一条过圆心的直线，该直线保证直线上方有N个点，直线下方有N个点，求出任意一条满足条件的直线即可。

直接暴力（-500，500）之间所有的a，b的值，满足条件直接输出即可

AC代码：

#include<bits/stdc++.h> 

using namespace std;

const int maxn = 3e5;

int n,upcnt,downcnt;
bool flag;
pair<int,int>cords[maxn];//pair存点坐标

int main(){
    while(cin >> n && n > 0){
        flag = false;
        for(int i = 0 ; i < 2*n ; i++) cin >> cords[i].first >> cords[i].second;
        for(int i = -500 ; i <= 500 ; i++){
            for(int j = -500 ; j <= 500 ; j++){
                upcnt = downcnt = 0;
                if(i == 0 && j == 0) continue;//如果a，b都为0就无法构成直线了
                for(int k = 0 ; k < 2*n ; k++){
                    int x = cords[k].first,y = cords[k].second;
                    if(i*x+j*y < 0) downcnt++;//计算直线下方的点数量
                    else if(i*x + j*y > 0)upcnt++;//计算直线上方的点数量
                }    
                if(downcnt == upcnt && downcnt + upcnt == 2*n){
                    cout << i << " " << j << endl;
                    flag = true;
                    break;
                }
            }
            if(flag)break;
        }    
    }
    return 0;
}

B - Is This Integration ?

In the image below you can see a square ABCD, where AB = BC = CD = DA = a. Four arcs are drawn taking the four vertexes A, B, C, D as centers and a as the radius. The arc that is drawn taking A as center, starts at neighboring vertex B and ends at neighboring vertex D. All other arcs are drawn in a similar fashion. Regions of three different shapes are created in this fashion. You will have to determine the total area if these different shaped regions.

Input

The input file contains a floating-point number a (0 ≤ a ≤ 10000) in each line which indicates the length of one side of the square. Input is terminated by end of file.

Output

For each line of input, output in a single line the total area of the three types of region (filled with different patterns in the image above). These three numbers will of course be floating point numbers with three digits after the decimal point. First number will denote the area of the striped region, the second number will denote the total area of the dotted regions and the third number will denote the area of the rest of the regions.

Sample Input

0.1
0.2
0.3

Sample Output

0.003 0.005 0.002
0.013 0.020 0.007
0.028 0.046 0.016

题目分析：

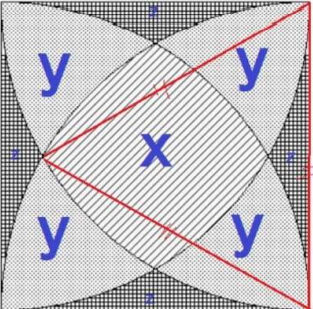
AC代码：

#include<iostream>
#include<cmath>
#include<cstdio>

using namespace std;

double a,x,y,z;

int main(){
    while(cin >> a){
        z = a*a - sqrt(3.0)/4.0*a*a-acos(-1.0)/6.0*a*a;
        y = (-1.0+sqrt(3.0)/2.0+acos(-1.0)/12.0)*a*a;
        x = (1.0-sqrt(3.0)+acos(-1.0)/3.0)*a*a;
        printf("%.3f %.3f %.3f\n",x,4*y,4*z);
    }
    return 0;
}

C - Simple division

Integer division between a dividend n and a divisor d yields a quotient q and a remainder r. q is the integer which maximizes q ∗ d such that q ∗ d ≤ n and r = n − q ∗ d. For any set of integers there is an integer d such that each of the given integers when divided by d leaves the same remainder.

Input

Each line of input contains a sequence of nonzero integer numbers separated by a space. The last number on each line is 0 and this number does not belong to the sequence. There will be at least 2 and no more than 1000 numbers in a sequence; not all numbers occuring in a sequence are equal. The last line of input contains a single 0 and this line should not be processed.

Output

For each line of input, output the largest integer which when divided into each of the input integers leaves the same remainder.

Sample Input

701 1059 1417 2312 0
14 23 17 32 122 0
14 -22 17 -31 -124 0
0

Sample Output

179
3
3

问题分析：

如果满足两个数字mod同一个数字得出的余数相同，那就说明这两个数字的差一定是那个数字的倍数。

所以先差分，求差分后的数字的最小公倍数即可

AC代码：

#include<bits/stdc++.h>

using namespace std;

const int maxn = 1e4+5;
int cnt,ans,a[maxn],f[maxn];

int gcd(int a,int b){
    return b == 0 ? a : gcd(b,a%b);
}

int main(){
    while(1){
        cnt = 0,ans = 0;
        while(cin >> a[cnt] && a[cnt] != 0) cnt++;
        if(cnt == 0 && a[cnt] == 0) return 0;
        for(int i = 1; i < cnt ; i++){
            ans = gcd(ans,abs(a[i] - a[i-1]));
        }
        cout << ans << endl;
    }
    return 0;
}

D - Euclid Problem

From Euclid it is known that for any positive integers A and B there exist such integers X and Y that AX + BY = D, where D is the greatest common divisor of A and B. The problem is to find for given A and B corresponding X, Y and D.

Input

The input will consist of a set of lines with the integer numbers A and B, separated with space (A, B < 1000000001).

Output

For each input line the output line should consist of three integers X, Y and D, separated with space. If there are several such X and Y , you should output that pair for which |X| + |Y | is the minimal. If there are several X and Y satisfying the minimal criteria, output the pair for which X ≤ Y .

Sample Input

4 6
17 17

Sample Output

-1 1 2
0 1 17

问题分析：

扩展欧几里得定理的模板题

AC代码：


#include<bits/stdc++.h>

using namespace std;

int a,b,d,x,y;
void exgcd(int a,int b,int &d,int &x,int &y){
    if(b == 0){
        d = a;
        x = 1;
        y = 0;
    }
    else{
        exgcd(b,a%b,d,y,x);
        y-=x*(a/b);
    }
}

int main(){
    while(cin >> a >> b){
        exgcd(a,b,d,x,y);
        cout << x << " " << y << " " << d << endl;
    }
    return 0;
}